
Propongo en esta entrada un adictivo puzle ideal para ejercitar nuestras neuronas en vacaciones.
Se cuenta que Piet Hein -artista, matemático y creador de juegos como el Hex- estaba en una conferencia de Heisemberg (el verdadero, Werner, no el prota de Breaking Bad) y que dejó volar su imaginación pensando en cubitos:
Hay un tricubo y 6 tetracubos irregulares eso hace 3 + 6×4 = 27 cubitos, ¡veintisiete! Eso son tres al cubo ¿se podrá montar con ellos un cubo con tres cubitos de arista?
Y sí, sí que se puede, como Conway y Guy probaron años después, hay 240 formas (dejo a Clara Grima, David Orden o cualquiera de sus discretos colegas que comprueben si Conway estaba en lo cierto)
Pero empecemos con lo de los tricubos y tetracubos irregulares que ya tiene un taller de matemáticas.
¿Cuántos formas distintas se pueden hacer con un solo cubo? Parece una pregunta trampa pero la respuesta es simple, una, el propio cubo. ¿Y con dos? Una también. Uno encima del otro (se puede poner de pie o tumbado pero estaremos de acuerdo en que es la misma forma, eso se llama en matemáticas ser invariante por giros) ¿Y con tres cubitos?Algo más de variedad, se llaman tricubos y se pueden hacer… dos, incluso les podemos poner nombre, «el palo y la r», para los que no se lo imaginan les recomiendo que vean menos televisión que vean la siguiente imagen:

Si pasamos a cuatro cubitos (tetracubos) la cosa se pone más interesante, además del palo y del cuadrado, que son los únicos convexos (las líneas que unen puntos de su interior se quedan en su interior), surgen los seis «irregulares» o cóncavos.

¿Y no hay más? Pues no, y los que recuerden que en el tetris había dos L’s y dos N es porque eran tetraminós y no tetracubos, esto es, porque eran planos y no podían girarse en esa dirección (porque para eso tendrían que salir del plano). De hecho para pasar de una L a la otra se podía hacer una reflexión en un espejo, cosa que ahora sigue sin estar permitida, nótese que las dos piezas con forma de torre la azul y la roja son -salvando el color- reflejo una de la otra.
Así que ya tenemos nuestros siete tricubos y tetracubos irregulares (no convexos):
Para nombrarlos hemos usado el código de colores y números que usó Conway, 1 B (brown), 2 Y (yellow), 3 G green, 4 O (orange), 5 U (blue), 6 R (red), 7 A (black). Pero mi consejo es que si lo haces en clase o con niños les deis vuestros propios nombres, es un ejercicio muy divertido.
Para elaborar este cubo he utilizado mis adorados cubitos encajables o multilink que hemos podido ver aquí en varias ocasiones (edificios, sudokus). Aunque es fácil encontrarlo en tiendas fabricado en madera, lo que nos da la idea de que podría ser un buen trabajo para clase de tecnología (si las nuevas leyes dejan algo de ella). Con un poco más de maña se podría hacer de punto:

O con módulos sonobe:
En el vídeo anterior se observa que no solo cubos, con el SOMA se construyen figuras, convirtiéndose así en un auténtico Tangram 3D:

Mi principal dificultad en el momento en que me enfrenté al puzle no fue la de obtener una solución (sale más o menos rápidamente por ensayo y error, y con la práctica salen más rápido) sino encontrar un método para distinguirlas (y que no fuera fotografiarlas con el móvil). Es un ejercicio mental de primera categoría que no voy a evitaros hacer a los que no os contentéis con una solución y queráis ir a por las restantes 239. Un buen consejo es el de ver las formas en que se pueden colocar las «piezas difíciles» y luego rellenar huecos. Otra idea interesante es la de representar en papel isométrico las soluciones que vayamos obteniendo.
¿Os animáis? Mandad al grupo de facebook o a la cuenta de twitter las soluciones y figuras obtenidas y las compartiremos.
No dejéis de tocar las mates.

 Premio Bitacoras.com
Premio Bitacoras.com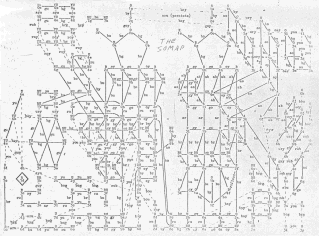





4 comentarios sobre “El cubo soma”