Vuelve tocamates, vuelve nuestro consultorio, Aló, tocamates. Ésta vez es una pregunta sobre ángulos que nos hace una clase de quinto de primaria de la Comunidad de Madrid, a través de su maestra, Ana, a la que conocí en un curso de formación:
¿Por qué las unidades menores de un ángulo se miden en minutos y segundos?
Para responder a esta pregunta hay que hacer un poco de historia. El sistema de medida de los ángulos se lo debemos a los babilónicos. Éstos heredaron la forma de contar que tenían sus antepasados sumerios, tal día como hoy hace 4000 años.
Los sumerios contaban en base 12, como aún hacemos nosotros con los huevos cuando los contamos por docenas. El otro día estaba en un bar -pidiendo precisamente un pincho de tortilla- cuando llamó el proveedor de huevos, la respuesta de cocina fue ¡que traigan 30! Treinta huevos pueden ser muchos para tu colesterol o para el mío, pero no se referían a huevos, sino a docenas. Treinta docenas de huevos son 360 huevos. ¡Qué casualidad! Como los grados que tiene una circunferencia. ¿Pero por qué de 12 en 12?
Mírate la palma de la mano, la derecha si eres diestro, piensa que vas a usar el pulgar para contar, y que no vas a contar tus dedos, sino tus falanges, ¡vaya!, hay doce. Doce es un número muy conveniente para hacer repartos, porque da divisiones exactas cuando repartes entre 2, 3, 4, 6.
A los ancianos sumerios les gustaba mirar al cielo, tanto como a mí mirar al suelo. Habían observado que el tiempo que tardaba la Luna en pasar por todas sus fases era de 29,5 días*. Como contaban de doce en doce, doce lunas daba un poco menos de 360 días, era razonable asignar a un año el valor de esas doce lunas. También, por eso, pensaron en las doce casas del horóscopo, aunque eso no fuera tan razonable. Por cierto, que los egipcios también tenían un calendario de 360 días, aunque sabían que duraba 365, arreglaron esa disparidad inventando las vacaciones de 5 jornadas que no contaban.
 Los babilonios heredaron la base doce, y la ampliaron. La hipótesis más plausible es que además de contar las falanges de una mano, como tenían la otra libre, marcaran un dedo en la otra cada vez que se completara una docena. Cinco veces doce hace ¡sesenta! Un número muy bueno para ser una base, porque da divisiones exactas también cuando se reparte entre 5 (y entre muchos más). Por cierto, ¿cuántos divisores tiene 60? ¿es el primero en tener ese número de divisores?. Aún se puede ver a gente contando así en oriente medio o en Afganistán, según me han contado.
Los babilonios heredaron la base doce, y la ampliaron. La hipótesis más plausible es que además de contar las falanges de una mano, como tenían la otra libre, marcaran un dedo en la otra cada vez que se completara una docena. Cinco veces doce hace ¡sesenta! Un número muy bueno para ser una base, porque da divisiones exactas también cuando se reparte entre 5 (y entre muchos más). Por cierto, ¿cuántos divisores tiene 60? ¿es el primero en tener ese número de divisores?. Aún se puede ver a gente contando así en oriente medio o en Afganistán, según me han contado.
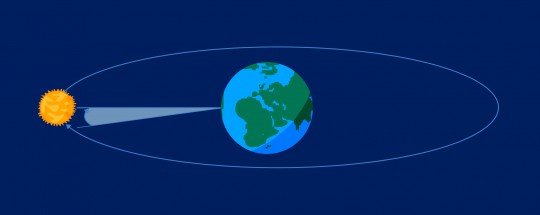
Nos hemos quedado mirando al cielo. Cuando se mira con detalle, se observa que el Sol va avanzando en el cielo. No sale todos los días por el mismo lugar, sino que va haciendo su recorrido, evolucionando sobre el fondo de estrellas que permanecen fijas**. Nosotros sabemos que esto no es así, que es la Tierra la que gira alrededor del Sol, pero si obviamos ese pequeño detalle y nos fijamos en la curva aparente que realiza, es una vuelta completa a nuestro cielo, y una vuelta que toma todo un año. Si un año tiene 360 días (ya tú sabes, más o menos), cada día del año evolucionará 1/360 partes de esa vuelta, es muy razonable decir que cada una de esas partes es un grado, y de ahí llegar a que cualquier círculo tiene 360 partes es un razonable proceso de generalización. Sobre el nombre de los “grados” para medir ángulos, decir que gradi era “andar” en latín, y gradus era “paso”. Todo encaja.
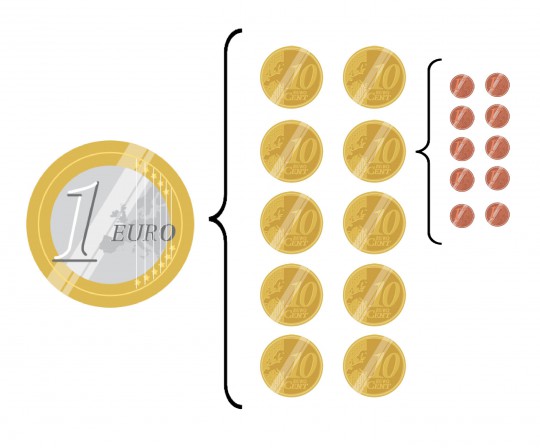
Todavía no sabemos por qué los ángulos se miden en minutos y segundos, pero está llegando, piénsalo. ¿Qué hacían los babilónicos cuando había que dividir algo y no daba exacto? Pues exactamente lo mismo que nosotros, considerar unidades más pequeñas. Imagina que quieres repartir 3 euros entre cuatro personas, como no da exacto lo que haces es pasarlo todo a céntimos, 300 céntimos si que se pueden repartir entre cuatro, a cada uno le corresponden 75 céntimos. La única diferencia es que en lugar de nuestro sistema decimal (base diez) el suyo era sexagesimal base 60), como hemos visto. Por eso no es nada extraño que cada grado de los ángulos estuviera dividido en 60 partes menudas o minutos y que de haber necesidad de precisar más, cada una de estas partes se subdivida en segundos, que son los que siguen a los primeros. Como no precisaban partes más pequeñas (no tenían aparatos de mayor precisión) no tenemos terceros y para cuando se tuvo la necesidad -marcada por la precisión- de subdividir los segundos ya no se utilizaba la base 60, por eso cuando subdividimos segundos volvemos a la base 10 y tiramos de décimas, centésimas y milésimas, como hacemos con el sistema monetario.
Espero que la respuesta satisfaga a la clase de Ana, y que arroje algo de luz sobre la medida de ángulos y sus unidades. No dudes en mandar tus propias preguntas, dejándolas como comentario o enviándolas a través del formulario.
No dejes de tocar las mates.
*El tiempo que tarda la Luna en completar una vuelta alrededor de la Tierra es de 28 días (mes sideral), pero como en esos días ambas giran alrededor del Sol, no vuelve a su fase original hasta transcurridos 29,5 días (mes sinódico).
**Como me cuenta mi amigo Javier Armentia, que curra mirando al cielo porque es astrofísico y director del Pamplonetario, mirar al Sol y las estrellas para configurar el calendario tiene todo el sentido del mundo:
Evidentemente, no se ve el sol a la vez que las estrellas pero podemos fijarnos en la última estrella que se ve antes de que salga el sol. Es lo que se dice el «orto helíaco». Y se sabe de su uso como marcador del calendario, por ejemplo en Egipto el orto helíaco de Sirio anunciaba la crecida del Nilo. En Roma anunciaba la caló, de ahí lo de la canícula precisamente (Sirio es la estrella del perro o can).

 Premio Bitacoras.com
Premio Bitacoras.com



9 comentarios sobre “Aló, Tocamates: ¿por qué medimos los ángulos en grados, minutos y segundos?”