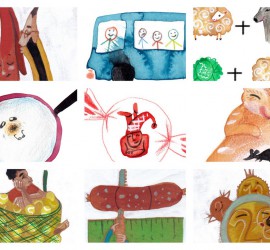
Matemáticas con pinzas 6
Las matemáticas son para el verano, y qué mejor que hacerlas con materiales manipulables, cuando cae la tarde y ya no hace tanto calor, si es posible a la orilla del mar o de la piscina. Traigo con esta entrada una propuesta para que no dudéis en hacer matemáticas con materiales cotidianos -no es la … Seguir leyendo »
6 comentarios.
 Premio Bitacoras.com
Premio Bitacoras.com