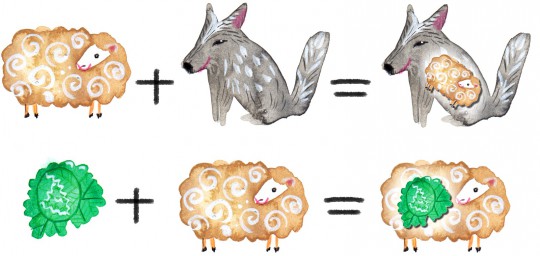
Un pastor vuelve del mercado con sus últimas adquisiciones, un perro lobo, una oveja y una lustrosa col, al ir a pasar el río encuentra que hay una balsa que sólo le permite pasar con uno de los animales o con la col, sabemos que el lobo devoraría a la oveja en cuanto se encuentren a solas y que la oveja se comería la col al mínimo descuido del pastor. ¿Puedes explicarnos cómo lo consiguió?
Este es el problema de esta semana. Se plantea los viernes en el blog y en Radiosol XXI, que emite en el 99.8 de Madrid y para todos en streaming. Y viene acompañado de una preciosa ilustración de Clara Varela. Los lunes lo resolvemos en directo a las 8.30 de la mañana en el programa despertador infantil DiverClub. Si quieres dar tu solución en directo -y eres un niño o niña- puedes escribirles a [email protected].
El de arriba es el enunciado que más consenso encuentra entre las versiones «occidentales» de los problemas de «cruzar el río». Se dice que Alcuino de York (mentor de Carlomagno, s. VIII) lo habría incluido en el libro «Propositiones ad acuendos juvenes» (proposiciones para retar a los jóvenes) que escribió (aquí el texto en latín). Hay muchísimas otras versiones, en África lo cuentan sólo que protagonizado por una pantera, un cerdo y unas gachas, mientras que en dinamarca hay una versión con un zorro, un ganso y una mazorca de maíz. En ningún caso explican por qué un pastor pudo querer comprar un lobo, un zorro o una pantera.
Como es un problema bastante conocido a los mayores les traigo de bonus la siguiente variante, del mago del acertijo, genio y embaucador Sam Loyd:

Las cuatro fugas
En algún momento pasado, a juzgar por sus ropajes, cuatro solteros celosos se fugaron con sus también celosas amadas. En su huída se vieron forzados a cruzar un caudaloso río en un bote que sólo podía -una vez más- acarrear a dos personas por viaje. En mitad de la corriente, tal como muestra la ilustración, había una pequeña isla. Parece que los jóvenes eran tan celosos que ninguno de ellos permitía que su futura esposa permaneciera ni un segundo en compañía de otro hombre u hombres a menos que también él estuviese presente.
Tampoco ninguno de ellos estaba dispuesto a embarcarse solo en el bote cuando hubiera una muchacha sola, en la isla o en la costa, si esta muchacha no era aquella con la que estaba comprometido. Esto confirma que ellas también eran celosas, ya que temían que sus compañeros huyeran con alguna de las otras si se les daba la oportunidad. Así las cosas, el problema consiste en descubrir cuál es la manera más rápida de hacer cruzar el río a todo el grupo.
¿Cuántos viajes debe hacer el bote para cruzar a todas las parejas según las condiciones impuestas?
No uses los comentarios para dar la solución (porque la borraré :P), puedes pedir o dar pistas, contar cómo te ha ido o proponer otros problemas.
No dejes de tocar las mates. Recuerda que puedes seguirnos por email (TocaMates en tu email) o en Facebook.
A la edición 3,1415926535 del Carnaval de Matemáticas, que en esta ocasión acoge @monzonete en su blog La aventura de la ciencia.

 Premio Bitacoras.com
Premio Bitacoras.com



14 comentarios sobre “Cruzando el río”